细粉加工设备(20-400目)

我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。

MTW系列欧版磨粉机

稀油润滑系统，新型吊挂式笼式选粉机结构设计

LM立式辊磨机

采用新型碾磨装置自动化电控系统

5X系列欧版智能磨粉机

大型规模化环保智能磨粉机优选设备

LM矿渣立式磨

LM矿渣立式磨集破碎、干燥、粉磨、分级输送于一体

立式磨煤机

烘干与制粉二合一可边磨边烘干

雷蒙磨粉机

工业磨粉设备先驱，经济实用

更多了解

超细粉加工设备(400-3250目)

LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。

LUM超细立磨

LUM超细立磨结合现代磨粉理念

MW环辊微粉磨

采用新型碾磨装置自动化电控系统

粗粉加工设备(0-3MM)

兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。

LM砂粉立磨

大型效率与节能双高型砂粉制备产品

AD平分∠BAC

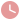
如图,在 ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB

AD平分∠BAC, 结果一题目如图,在 ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB=6,AC=14,∠ABC=3∠C,则BE=A EC DB 答案 [分析]如图延长交于证明可得再解析（1）证明：∵ ∠ B+∠ C=180°，∠ B=90°， ∴ ∠ B=∠ C=90°， ∵ AD平分∠ BAC， ∴ ∠ DAC=∠ DAB，在 ADC和 ADB中，\ ( (array)l∠ DAC=∠ DAB∠ C=∠ BAD=AD (array)， ∴ 感知：如图①，AD平分∠ BAC，∠ B+∠ C=180°，∠ B=90

如图，在 ABC中，AD平分∠BAC，交BC于点D，CE⊥AD于

如图，在 ABC中，AD平分∠BAC，交BC于点D，CE⊥AD于点E，∠B＝∠ECD，若CE＝3，CD＝4，则AC＝解：A F E B G D C延长CE交AB于点F，过点F （1）由于AD平分∠BAC，根据角平分线的概念可得∠BAD=∠CAD，再根据三角形的一个外角等于和它不相邻的两个内角和，结合已知条件可得∠EAC与∠B相等；如图，AD平分∠BAC，∠EAD=∠EDA．（1）∠EAC与∠B

如图，AD平分∠BAC，∠EAD=∠EDA，∠B=50° Baidu

【答案】（1）50°；（2）48°【解析】【分析】（1）根据∠EAD＝∠EDA，利用角度关系与外角定理得到∠EAC+∠CAD＝∠B+∠BAD，由AD平分∠BAC得到∠CAD＝∠BAD，于在线课程分析【感知】根据角平分线的性质，欲证明DB=DC，只要证明DC⊥AC，DB⊥AB即可；【探究】作DN⊥AC于N，DM⊥AB于M，欲证明DB=DC，只要 [感知]如图1AD平分∠BAC∠B+∠C=180°∠B=90°求证

如图， ABC中，AD平分∠BAC，DE⊥AB于点E，S ABC=15

如图， ABC中，AD平分∠BAC，DE⊥AB于点E，S ABC=15，DE=3，AB=6，求AC的长A EB DC 答案解：∵DE=3，AB=6，∴S ABD=12×3×6=9∵S ABC=S ABD+S ACD，S 2011年10月15日结论有误,应该是:AB/AC=BD/DC 证法1:作DE平行CA,交AB于E,则⊿BED∽⊿BAC;且∠EDA=∠DAC; 又∠EAD=∠DAC,故∠EAD=∠EDA,AE=DE 已知 ABC中,AD是角BAC的角平分线,求证AB/AC=BC/DC

如图，在 ABC中，AD平分∠BAC．雨露学习互助

如图，在 ABC中，AD平分∠BAC．（1）若AC=BC，∠B：∠C=2：1，试写出图中的所有等腰三角形，并给予证明．（2）若AB+BD=AC，求∠B：∠C的比值．探究：如图2，AD平分∠BAC，∠ABD+∠ACD=180°，∠ABD＜90°，求证：DB=DC ．应用：如图3，四边形ABCD中，∠B=45°，∠C=135°，DB=DC=a，则AB﹣AC= （用含a的代数式表示）试题答案练习册答案在线课程练习册系列答案课堂在线系列答案感知:如图1AD平分∠BAC．∠B+∠C=180°∠B=90°易知

如图，在 ABC中，∠ABC=2∠C，AD平分∠BAC，求证

题目如图,在 ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=ACA CD B 答案 [答案]证明见解析 [解析] [分析]在AC上截取AE=AB,利用“边角边”证明 ABD和 AED全等,根据全等三角形对应边相等可得DE=BD,全等三角形对应角相等可得∠AED=∠ABC,然后求出∠C=∠CDE,根据等角对等边可得CE=DE 1 (此题总分值10分 )如图, ABC中, AD平分∠BAC, 且DB =DC, DE⊥AB于E, DF⊥AC于F, (1 )求证:∠ABD与∠ACD互补; (2 )如果AB=8, AC=6, 求AE, BE的长 2 如图，\triangle ABC中，AD平分∠BAC，且DB=DC，DE⊥AB于E，DF⊥AC于F， (1)求证：∠ABD与∠ACD互补； (2)如果AB=8，AC=6，求AE，BE的长．收藏如如图， ABC 中， AD 平分 ∠BAC ，且 DB=DC ， DE⊥AB

如图，在Rt ABC中，∠C=90°，AD平分∠BAC，交BC于点D

tanB = 结果一题目如图，在Rt ABC中，∠C＝90°，AD平分∠BAC，交BC于点D，DC=， AC=3．（1）求∠B的度数；（2）求AB及BC的长．答案【答案】（1）30°；（2）AB=6，BC=．试题分析：（1）由tan∠DAC=，得出∠DAC30°，再由角平分线的性质得到∠BAD=30°，根据直角三角形如图，在三角形ABC中，AD为∠BAC的平分线，DE垂直AB于E，DF垂直AC于F，三角形ABC面积是28cm ，AB=20cm,AC=8cm,求DE的长答案因为 AD是角BAC的平分线所以角BAD＝角DAC又因为 DE垂直AB，DF垂直AC 所以角AED＝角AFD＝90度所以三角形ADE与三角形ADF全等所以 DE=DF 因为三角形ABC 如图，在三角形ABC中，AD为∠BAC的平分线，DE垂直AB于

如图，已知 ABC的面积为12，AD平分∠BAC，且AD⊥BD于

题目【题目】如图，已知 ABC的面积为12，AD平分∠BAC,且AD⊥BD于点D,则 ADC的面积是 ()A dD BC A10 B8 C6 D4 答案【解析】 A E D B C 如图，延长BD交AC于点E, :AD平分∠BAE,AD⊥BD, ∴∠BAD=∠EAD,∠ADB=∠ADE, 在 ABD和 AED中， ∠BAD=∠EAD AD=AD ∠BDA=∠EDA ∴ ABD≡ AED (ASA), ∴BD=DE 如图①,在 ABc中,AD平分∠BAc,AE⊥Bc,∠B=40°,∠c=70° (1)求∠DAE的度数; (2)如图②,若把“AE⊥Bc”变成“点F在DA的延长线上,FE⊥Bc”,其它条件不变,求∠DFE的度数相关知识点：三角形三角形基础三角形有关的角三角形内角和定理三角形内角和定理直接求解试题如图①,在 ABc中,AD平分∠BAc,AE⊥Bc,∠B=40°,∠c=70°(1

C、D两点在以AB为直径的半圆周上，AD平分∠BAC,AB=20

题目 C、D两点在以AB为直径的半圆周上，AD平分∠BAC,AB=20，AD=4\sqrt {15}，则AC的长为相关知识点：试题来源：解析 4 试题分析：连接OD，OC，作DE⊥AB于E，OF⊥AC于F，证明 AOF≌ ODE，设AC=2x,则OE=AF=x,应用勾股定理计算即可。解：连接OD，OC，作DE⊥AB于E 解析如图,在 ABC中,AD是∠BAC的平分线,延长AD至E,使AD=DE,连接BE,若AB=3AC, BDE的面积为9,则 ABC的面积是 ( ) A6 B9 C12 D15 [分析]过点D作DG⊥AB于G,DF⊥AC,交AC延长线于F,利用角平分线的性质可得DG=DF,再运用等高的两个三角形面积比等于底之比即可得如图,在 ABC中,AD是∠BAC的平分线,延长AD至E,使AD=DE

如图， ABC中，AB=2AC,AD平分∠BAC，且AD=BD,求证

2012年9月16日做DE⊥AB于E即∠AED=90° ∵AD=BD ∴ ABD是等腰三角形 ∴DE是等腰三角形底边AB上的中线（等腰三角形三线合一）即AE=BE=1/2AB ∵AB=2AC即AC=1/2AB ∴AE=AC ∵AD平分∠BAC解得：x=16． ∴∠E=48°．（1）由于AD平分∠BAC，根据角平分线的概念可得∠BAD=∠CAD，再根据三角形的一个外角等于和它不相邻的两个内角和，结合已知条件可得∠EAC与∠B相等；（2）若设∠CAD=x°，则∠E=3x°．根据（1）中的结论以及三角形的内角如图，AD平分∠BAC，∠EAD=∠EDA．（1）∠EAC与∠B

[感知]如图1AD平分∠BAC∠B+∠C=180°∠B=90°求证

∴AD平分∠BAC．点评本题考查全等三角形的判定和性质、角平分线的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形，属于中考常考题型．结果四题目【题目】如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,EBDAFC (1)求证:EB=FC; (2)若∠BAC=45°,求∠BDC的度数; (3)若四边形ABDC的面积为8,AB=3,AC=5,求DF的长答案【解析】 (1)证明:AD平分∠BAC,DE⊥AB于EDF⊥AC于F,DE=DF,∠BED=∠CFD=90°在Rt BDE和Rt CDF中,DB=DCDE= Rt BDERt CDF (HL 如图， AD 平分 ∠BAC ， DE⊥AB 于 E ， DF⊥AC 于 F

在 ABC中，∠BAC=90°，AB=3，AC=4．AD平分∠BAC交BC

在 ABC中,∠BAC=90°,AB=3,AC=4,AD平分∠BAC交BC于D,则BD的长为( )C D A BA15 7 B12 5 C20 7 D21 5[考点]角平分线的性质;三角形的面积;勾股定理[分析]根据勾股定理列式求出BC,再利用三角形的面积求出点A到BC上的高,根据角平分线上的点到如图， ABC内接于⊙ O，AD平分∠ BAC交BC边于点E，交⊙ O于点D，过点A作AF⊥ BC于点F，设⊙ O的半径为R，AF=h．（1）过点D作直线AF=h ，求百度试题结果1 结果2 题目如图， ABC内接于⊙ O，AD平分∠ BAC交BC边于点E，交⊙ O于点D，过点A 如图， ABC内接于⊙ O，AD平分∠ BAC交BC边于点E，交⊙

如图, ABC的面积为16,AD平分∠BAC,且AD⊥BD于点D,则

题目如图, ABC的面积为16,AD平分∠BAC,且AD⊥BD于点D,则 ADC的面积是 ( ) A 6 B 8 C 10 D 12 相关知识点：全等三角形全等三角形的基本应用三角形的角平分线角平分线的性质角平分线的性质应用试题来源：详见解析[解析][分析]先由角平分线的性质得DE=DF,通过证明 BDE≌ CDF可得∠B=∠C,然后根据三角形三线合一的性质即可解答[详解]证明:∵AD平分∠BAC, DE⊥AB,DF⊥AC,∴DE=DF,∠BED=∠CFD=90,又∵D是BC中点,∴DB=DC,在R 如图,在 ABC中,AD平分∠BAC,D是BC中点,DE⊥AB,DF⊥AC

知乎专栏随心写作，自由表达知乎

知乎专栏是一个自由写作和表达平台，让用户随心所欲地分享观点和知识。2 如图，AD平分∠BAC，CD⊥AD于点D，图中∠1与∠2、∠B之间有一种数量关系始终保持不变，给出这一数量关系，并说明你的理由 3 【题目】如图,AD平分∠BAC,CD⊥AD于点D,图中∠1与∠2、∠B之间有一种数量关系始终保持不变,给出这一数量关系,并说明你的如图，AD平分∠BAC，CD⊥AD于点D，图中∠1与∠2、∠B

如图,已知 ADC的面积为4,AD平分∠BAC,且AD⊥BD于点D

题目如图,已知 ADC的面积为4,AD平分∠BAC,且AD⊥BD于点D,那么 ABC的面积为相关知识点：全等三角形全等三角形的基本应用三角形的角平分线角平分线的性质角平分线的性质应用试题来源：探究：如图2，AD平分∠BAC，∠ABD+∠ACD=180°，∠ABD＜90°，求证：DB=DC ．应用：如图3，四边形ABCD中，∠B=45°，∠C=135°，DB=DC=a，则AB﹣AC= （用含a的代数式表示）试题答案练习册答案在线课程练习册系列答案课堂在线系列答案感知:如图1AD平分∠BAC．∠B+∠C=180°∠B=90°易知